KNOW YOUR ROULETTE ODDS
Roulette odds provide you with the information you need to know how likely you are to win any bet. There are many different bets available on a roulette table, and each one has its own odds. These range from even money bets that pay off nearly half the time, to single number bets that are hard to hit, but which will earn you a lot of money when they do.
- The betting odds in roulette of hitting a single number with a straight-up bet are 37 to 1, since there are 38 numbers (1 to 36, plus 0 and 00). However, the house only pays out 35 to 1 on winning.
- Roulette inside bets Inside bets are the riskiest bets that can be placed during a game of roulette with the decreased odds of winning, but increased profits if correctly predicted. Single number bet – A single number bet stands as the riskiest bet that can be made during a game of roulette with a 35/1 payout.
- The winning odds for those bets is 32.43% in European Roulette, and 31.58% in the American version. Consecutively, this bet will bring you more winnings – the payout for Column and Dozen is 2:1. Odds & Payouts for Inside Bets Inside bets include betting on a single number, or on a small group of them.
Every roulette table will have a betting limit and this is where it becomes important to understand the rules for combing the inside and outside bets. If the limit is set to $5 you can’t spread this sum over the inside and outside bets. You will either put the $5 on the inside bets or on the outside.
Before diving deeper into roulette odds, however, it’s important that you understand the basics of how to play roulette. Before every spin, you will have the opportunity to place as many bets as you like all around the roulette table. Each of these bets covers one or more of the numbered pockets on the roulette wheel, and comes with its own specific odds of winning.
When the croupier spins the ball around the wheel, it will eventually fall into one of these pockets. The number and color of that pocket will determine which bets win on that spin. At this point, the croupier will mark the winning number, losing bets are taken off the table, and roulette payouts are made for the remaining winning bets before the next spin.
AMERICAN VS. EUROPEAN ROULETTE PROBABILITIES
While the American and European games may seem similar at first glance, the two games actually use different roulette wheels. The American wheel has both a zero (0) and a double zero (00) on it, while the European wheel only has the single zero.
This actually makes a major difference to players. European roulette odds are much better for players, because there is one less pocket on the wheel for the ball to fall into. Since both versions offer the same roulette payouts, this means that the odds and house edge are smaller in European roulette.
Some European roulette games offer additional rules that further help the player cut into the house edge. When a casino offers la partage, that means that you will only lose half of an even money bet (meaning bets like odd/even or red/black) if the ball lands on zero.

En prison is a variation of the la partage rule. Rather than getting half of your bet back, the money will instead be put “in prison”. after which you can win it all back If the next spin results in a win for that bet. In either case, these options offer the best odds in roulette, as they cut the house edge roughly in half.
EUROPEAN | AMERICAN | |
| NO | DOUBLE ZERO | YES |
| 37 | NUMBER OF SECTORS | 38 |
| 2.7% | HOUSE EDGE | 5.26% |
| 97.3% | AVERAGE PAYOUT FOR 100 € | 94.74% |
ROULETTE ODDS AND PAYOUTS EXPLAINED
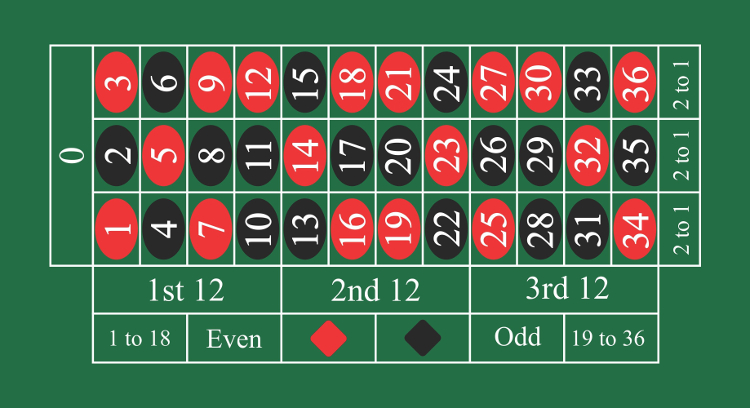
While there are a wide array of roulette bet types to choose from, these options can mainly be divided into two types: inside bets and outside bets. These categories get their names based on where these bets occur on the roulette table layout. Inside bets are placed on the numbers at the center of the table, while outside bets have special betting areas on the outer portion of the board.
Inside Bets
Inside bets tend to have a lower probability of winning, but they offer the biggest roulette payouts. For this reason, they are often the best way to start playing for those who are new to the game, as they give you a chance to earn a big payout on any given spin without having to risk much money on each bet.
Straight: A bet on a single number. If the ball lands on that number, the bet pays 35-1.
Split: A bet on two adjacent numbers on the roulette table. If either of those numbers hits, the bet pays 17-1.
Street: A bet on a row of three numbers on the roulette layout. If any of those numbers wins, your bet pays out at 11-1 odds.
Corner: A bet on a “square” of four numbers on the roulette betting layout. If any of these numbers wins, the bet pays 8-1.
Six Line: A bet on two consecutive rows, covering six numbers in total. If the ball lands on any of those numbers, you’ll win at 5-1 odds.
First Four: This bet is only available on European roulette tables, and covers the zero along with 1, 2, and 3. If any of those four numbers wins, the bet pays 8-1.
Trio: Like a street bet, this bet covers three numbers, but it includes one of the zeros. For instance, a player can make a trio bet covering 0, 1, and 2. If any of those numbers wins, the bet pays 11-1.
Top Line: This bet is only available on American roulette tables and covers five numbers in total: the zero, double zero, 1, 2, and 3. If the ball lands on any of those numbers, your bet pays out at 6-1 odds.
Outside Bets
Outside bets cover large sections of the wheel, giving you a better chance of winning your bet. However, they also come with smaller payouts, and may require higher minimum wagers than inside bets.
Columns: A column bet covers one of the three columns on the roulette table layout, each of which contains 12 numbers. If any of those 12 numbers wins, your bet pays 2-1 odds.
Dozens: These bets cover sets of 12 consecutive numbers: 1-12, 13-24, or 25-36. If a number in the range you bet on wins, the bet pays 2-1.
Odd/Even: These bets cover all of the odd or even numbers on the table (note that zeros do not count as either odd or even). If a matching number wins, then your bet pays out even money.
Red/Black: These bets cover all pockets – 18 each – of that color. If the ball lands on that color, you win at even money odds.
High/Low: These bets cover the range of 1-18 and 19-36. Should the ball land on a number in the range you’ve chosen, the bet pays even money.
Called & Announced Bets
Called and announced bets are roulette bet types that may not be familiar even to many experienced players. These are more frequently seen in European casinos, and they allow players to make bets by announcing them to the croupier. Called bets can be made on credit, while announced bets require a player to actually have the money on the table in order to make them.Typically, such bets are only offered to known players, usually high rollers. In modern roulette, announced bets are far more common than called bets, as most casinos cannot or will not allow their players to wager on credit.
While any bet can be an announced bet, this option is typically only used for complex wagers, most of which are known as the French bets. These bets cover specific portions of the roulette wheel, which takes several chips to accomplish and can be unwieldy to manage on the standard roulette betting layout. Instead, the croupier can manage those bets for players, sometimes by using the “racetrack” layout seen on some European roulette tables.
Common announced bets include:Voisins du Zero: This bet covers 17 numbers using nine chips. Your payout will be determined by the type of bet covering the winning number: 16 chips on the corner bet, 22 on the trio, or 17 chips if one of the splits wins.
Jeu Zero: The “zero game” covers just seven numbers using four chips. If a split wins, the bet will pay out 17 chips. If the number 26 hits, you win 35 chips.
Tiers du Cylindre: This bet covers 12 numbers that lie far away from the zero. It takes six split bets to cover these numbers, and you get a payout of 17 chips if any of them wins.
Orphelins: Made with five chips, this bet has varying payouts. The straight bet on 1 pays 35-1, while the split bets would pay 17-1.
Finals: A final bet covers every number that ends in a specific digit. These are all straight bets paying out at 35-1 odds.
Full Completes: A full complete is a true maximum bet on a single number. These bets involve heavy risks to the player, with the exact payouts depending on what number is hit, various table maximums, and which number is being maxed out.
You can find out more details on each of these on our called bets and announced bets page.
THE BEST ROULETTE BETS FOR YOUR BANKROLL
Our team of experts has years of experience playing roulette, meaning we know all the pro tips and tricks that can help you get the best roulette odds possible. One of the most important things we can share is how to make the best bets possible each time you step up to the roulette table. Here are our favorite bets in roulette:
THE WORST ODDS TO WATCH OUT FOR
While we’re happy to give you tips on how to find the best odds in roulette, the best thing we can do for our players is steer them away from bets that aren’t worth their time. By avoiding the worst of the worst options, you’ll improve your roulette odds and have more fun playing knowing you aren’t getting ripped off.
The biggest example is the Top Line or First Five bet on American roulette tables. While the odds in roulette are very consistent across almost all bets, this particular bet is an exception. This is because payouts in roulette are generally designed to be fair for a wheel with 36 pockets, with the house edge coming from the fact that there are actually 37 (European roulette) or 38 (American roulette) pockets for the ball to fall into.
On an American table, that means that whether you make a straight bet at 35-1 payout, or bet on black at even money, the house edge is 2/38, or 5.26%. However, the Top Line bet covers exactly five numbers (0-00-1-2-3), a number that 36 can’t be evenly divided into. Casinos offer 6-1 on this bet, which would only be a fair bet if there were 35 pockets. The result of this is a house edge of 7.89%, which is much higher than on any other bet.
The Top Line isn’t always the only sucker bet on the table. Generally, it’s best to avoid unusual side bets that may be added to the game, especially in online roulette. As in other casino games, these side bets are almost always added to make more money off players and come with extraordinarily high house edges.
HOW TO IMPROVE YOUR ODDS AT ROULETTE
One of the best ways to improve your odds in roulette is by brushing up on your roulette strategy. While the results of each spin are random, roulette strategies can be used to manage your sessions and get the kinds of results you’re looking for.
For instance, let’s say you want to maximize your chances of booking at least a small win at the end of a session. Your best bet may be the Martingale System, which asks you to place even money bets, doubling your bet amount after a loss. On the other hand, a player looking for a huge payday would be better off trying something like the Guetting System. We cover many of these systems as well as other ways to improve your odds on our roulette strategy page.
The most important thing you can do to maximize your roulette odds is to get some practice in before you try playing for real money. If you’re looking to develop your skills or test a new betting strategy, you’ll want to check out the 80+ free online roulette titles which are available for you to try without risking any money.
PLAY AT THE TOP ONLINE ROULETTE SITES
At this point, you should have a strong knowledge of roulette odds and payouts, which bets you want to seek out, and which to avoid. Armed with this information, you should feel confident about playing roulette for real cash at one of our top-rated casinos.
We only recommend the most trustworthy and reputable online casinos for our readers. Any of the sites in the table below will provide you with a safe and secure place to enjoy playing roulette.
| CASINO | BONUS | RTP | RATING | REVIEW | |
|---|---|---|---|---|---|
| 1 | T&C APPLY | PAYOUT | 10 | READ REVIEW | PLAY NOW |
| 2 | T&C APPLY | PAYOUT | 9.6 | READ REVIEW | PLAY NOW |
| 3 | T&C APPLY | PAYOUT | 9.3 | READ REVIEW | PLAY NOW |
| 4 | T&C APPLY | PAYOUT | 9 | READ REVIEW | PLAY NOW |
| 5 | T&C APPLY | PAYOUT | 9.4 | READ REVIEW | PLAY NOW |
FAQ
🎲 Are roulette odds good?
While roulette odds vary depending on the type of table you are playing at, the odds are generally quite good. That’s especially true when compared to other popular gambling options like slot machines, which normally have much higher house edges.
❤️ What is the best bet in roulette?
If you want the best odds in roulette, you’ll want to find a European roulette table where you can take advantage of la partage rules on even money bets. Under those conditions, the house edge is just 1.35%.
🎰 What are the best roulette bet combinations?
There are many different roulette bet combinations that are effective, with the best one depending on your goals at the table. Familiarizing yourself with bet systems can help you determine what works for you, and what doesn’t.
💰 How much is a roulette chip worth?
The most common value for a roulette chip in an American casino is one dollar. However, this amount can vary depending on how much you buy in for at the table. When you purchase your chips, your croupier will set a value that leaves you with a reasonable amount of chips to play with: buy in for $100, and you’ll get dollar chips; start with $10,000 on the table, and each chip might be worth $100 instead.
❓ Are roulette tables rigged?
Generally speaking, roulette tables are fair. Casinos have a mathematical advantage and don’t need to cheat to get roulette odds they are happy with. However, there have been plenty of cases where biased wheels have made some numbers appear more often than others – something that attentive players can take advantage of.
| CASINO | BONUS | RTP | RATING | REVIEW | |
|---|---|---|---|---|---|
| 1 | T&C APPLY | PAYOUT | 10 | READ REVIEW | PLAY NOW |
Introduction
The Gambler's Fallacy is the mistaken belief that if an independent event has not happened in a long time, then it becomes overdue and more likely. It is also equally incorrect that if an outcome has happened a disproportionate number of times lately, compared to statistical expectations, then it becomes overheated and less likely to occur the next time. An example of this fallacious thinking might be that if the number 23 hasn't been drawn in a 6-49 lottery the last 100 games, then it becomes more likely to be drawn during the next drawing.
Many worthless betting strategies and systems are based on belief in the Gambler's Fallacy. I got the idea for writing about this after reading an 888 online roulette article by Frank Scoblete entitled How to Take Advantage of Roulette Hot Spots. In that article, Scoblete recommends taking a count of each outcome for 3,700 spins in single-zero roulette and 3,800 spins in double-zero roulette in the hunt for 'hot numbers.' Never mind that this would take about 100 hours to make this many observations, assuming the industry standard of 38 spins per hour.
Before going further, let me say that I strongly believe modern roulette wheels made by top brands like Cammegh are extremely precise and any bias would be minuscule compared to the house advantage. Thus, testing a modern roulette for bias would be a total waste of time. Now, testing a 30-year-old hand-me-down wheel in a banana republic might be another story. However, you're on your own if you win a lot of money from said casino and try to leave with it.
That said, if you track 3,800 outcomes in single-zero roulette, the average number of times any number will hit is 3800/38=100. I ran a simulation of over 1.3 trillion spins, counting how many times each number was hit, sorting the outcomes to find the most frequent number and how many times it was observed, and keeping a count of how many times the most frequent number in each simulation was seen.
Hottest Number in 3,800 Spins of Double-Zero Roulette
As a former actuary, I hate to use a layman's term like the 'hottest number,' but that is how gamblers talk so will go with that. That said, following are the results of the count of the hottest number in millions of 3800-spin simulations.
Count of the Hottest Number in 3,800 Spins on Double-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 122.02 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
Here is what the table above means in plain simple English.
- The mean, or average, count of the hottest number is 122.02.
- The median count of the most frequent number is 121. This means that over 50% of time the most frequent number appeared 121 times or less, as well as 121 times or more. This is possible because the probability of 121 observations is in both groups.
- The mode, or most count of the hottest number is 120, which happens 8.29% of the time.
- The 90th percentile is the smallest number such that the probability the count of the hottest number is at least 90% .
- The 95th percentile is the smallest number such that the probability the count of the hottest number is at least 95%.
- The 99th percentile is the smallest number such that the probability the count of the hottest number is at least 99%.
- The 99.9th percentile is the smallest number such that the probability the count of the hottest number is at least 99.9%.
Hottest Number in 3,700 Spins of Single-Zero Roulette
The results are very similar with 3,700 spins tracked on a single-zero wheel. Following is a summary of the results.
Count of the Hottest Number in 3,700 Spins on Single-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 121.90 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
The following table shows the full results of the simulation on both wheels. The two commulative columns show the probability that the count of the hottest number is the number on the left column or more. For example, the probability the hottest number in 3,700 spins of single-zero roulette is 130 or more is 0.072044.
Summary of the Count of the Hottest Number in 3,700 Spins of Single-Zero Roulette and 3,800 spins of Double-Zero Roulette
| Count | Probability Single Zero | Cummulative Single Zero | Probability Double Zero | Cummulative Double Zero |
|---|---|---|---|---|
| 160 or More | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 159 | 0.000000 | 0.000001 | 0.000000 | 0.000001 |
| 158 | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 157 | 0.000001 | 0.000002 | 0.000001 | 0.000002 |
| 156 | 0.000001 | 0.000003 | 0.000001 | 0.000003 |
| 155 | 0.000002 | 0.000005 | 0.000002 | 0.000005 |
| 154 | 0.000003 | 0.000009 | 0.000003 | 0.000008 |
| 153 | 0.000005 | 0.000013 | 0.000005 | 0.000013 |
| 152 | 0.000007 | 0.000020 | 0.000008 | 0.000021 |
| 151 | 0.000012 | 0.000032 | 0.000012 | 0.000033 |
| 150 | 0.000017 | 0.000049 | 0.000018 | 0.000051 |
| 149 | 0.000026 | 0.000075 | 0.000027 | 0.000077 |
| 148 | 0.000038 | 0.000114 | 0.000041 | 0.000118 |
| 147 | 0.000060 | 0.000174 | 0.000062 | 0.000180 |
| 146 | 0.000091 | 0.000265 | 0.000092 | 0.000273 |
| 145 | 0.000132 | 0.000397 | 0.000137 | 0.000409 |
| 144 | 0.000195 | 0.000592 | 0.000199 | 0.000608 |
| 143 | 0.000282 | 0.000874 | 0.000289 | 0.000898 |
| 142 | 0.000409 | 0.001283 | 0.000421 | 0.001319 |
| 141 | 0.000580 | 0.001863 | 0.000606 | 0.001925 |
| 140 | 0.000833 | 0.002696 | 0.000860 | 0.002784 |
| 139 | 0.001186 | 0.003882 | 0.001215 | 0.003999 |
| 138 | 0.001652 | 0.005534 | 0.001704 | 0.005703 |
| 137 | 0.002315 | 0.007849 | 0.002374 | 0.008077 |
| 136 | 0.003175 | 0.011023 | 0.003286 | 0.011363 |
| 135 | 0.004355 | 0.015378 | 0.004489 | 0.015852 |
| 134 | 0.005916 | 0.021295 | 0.006088 | 0.021940 |
| 133 | 0.007939 | 0.029233 | 0.008196 | 0.030136 |
| 132 | 0.010601 | 0.039834 | 0.010908 | 0.041044 |
| 131 | 0.013991 | 0.053824 | 0.014384 | 0.055428 |
| 130 | 0.018220 | 0.072044 | 0.018757 | 0.074185 |
| 129 | 0.023498 | 0.095542 | 0.024114 | 0.098299 |
| 128 | 0.029866 | 0.125408 | 0.030603 | 0.128901 |
| 127 | 0.037288 | 0.162696 | 0.038228 | 0.167130 |
| 126 | 0.045771 | 0.208467 | 0.046898 | 0.214027 |
| 125 | 0.055165 | 0.263632 | 0.056310 | 0.270337 |
| 124 | 0.064853 | 0.328485 | 0.066020 | 0.336357 |
| 123 | 0.074178 | 0.402662 | 0.075236 | 0.411593 |
| 122 | 0.081929 | 0.484591 | 0.082885 | 0.494479 |
| 121 | 0.087158 | 0.571750 | 0.087696 | 0.582174 |
| 120 | 0.088520 | 0.660269 | 0.088559 | 0.670734 |
| 119 | 0.084982 | 0.745252 | 0.084406 | 0.755140 |
| 118 | 0.076454 | 0.821705 | 0.075245 | 0.830385 |
| 117 | 0.063606 | 0.885312 | 0.061851 | 0.892236 |
| 116 | 0.048069 | 0.933381 | 0.046111 | 0.938347 |
| 115 | 0.032432 | 0.965813 | 0.030604 | 0.968952 |
| 114 | 0.019117 | 0.984930 | 0.017664 | 0.986616 |
| 113 | 0.009567 | 0.994496 | 0.008614 | 0.995230 |
| 112 | 0.003894 | 0.998390 | 0.003420 | 0.998650 |
| 111 | 0.001257 | 0.999647 | 0.001065 | 0.999715 |
| 110 | 0.000297 | 0.999944 | 0.000243 | 0.999958 |
| 109 | 0.000050 | 0.999994 | 0.000038 | 0.999996 |
| 108 or Less | 0.000006 | 1.000000 | 0.000004 | 1.000000 |
Count of the Hottest Numbers in 300 Spins in Double-Zero Roulette
What if you don't want to spend 100 hours gathering data on a single wheel? Some casinos are kind enough to give you, on a silver platter, the number of times in the last 300 spins the four 'hottest' and 'coolest' numbers occurred. The image at the top of the page shows an example taken on a double-zero wheel at the Venetian.
In 300 spins, the average number of wins on a double-zero wheel for any number is 300/38=7.9. As you can see from the image above, the four hottest numbers were 20, 5, 29, and 2, which occurred 15, 14, 13, and 12 times respectively. Is this unusual? No. In a simulation of over 80 billion spins, the most frequent number, in 300-spin experiments, appeared most frequently at 14 times with a probability of 27.4%. The most likely total of the second, third, and fourth most frequent numbers was 13, 12, and 12 times respectively, with probabilities of 37.9%, 46.5%, and 45.8%. So the results of the 'hottest' numbers in the image above were a little more flat than average.
The following table shows the probabilities of the four hottest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.009210.
Count of the Hottest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000022 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000051 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000166 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000509 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.001494 | 0.000001 | 0.000000 | 0.000000 |
| 20 | 0.004120 | 0.000009 | 0.000000 | 0.000000 |
| 19 | 0.010806 | 0.000075 | 0.000000 | 0.000000 |
| 18 | 0.026599 | 0.000532 | 0.000003 | 0.000000 |
| 17 | 0.060526 | 0.003263 | 0.000060 | 0.000001 |
| 16 | 0.123564 | 0.016988 | 0.000852 | 0.000020 |
| 15 | 0.212699 | 0.071262 | 0.009210 | 0.000598 |
| 14 | 0.274118 | 0.215025 | 0.068242 | 0.011476 |
| 13 | 0.212781 | 0.379097 | 0.283768 | 0.117786 |
| 12 | 0.067913 | 0.270747 | 0.464748 | 0.457655 |
| 11 | 0.004615 | 0.042552 | 0.168285 | 0.383900 |
| 10 | 0.000017 | 0.000448 | 0.004830 | 0.028544 |
| 9 | 0.000000 | 0.000000 | 0.000001 | 0.000020 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary of the Count of the Four Most Frequent Numbers in 300 Spins of Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.48 | 14 | 14 |
| Second | 13.07 | 13 | 13 |
| Third | 12.27 | 12 | 12 |
| Fourth | 11.70 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Double-Zero Roulette
The next table shows the probability of each count of the four collest numbers in 300 spins of double-zero roulette.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.012679 | 0.000063 | 0.000000 | 0.000000 |
| 1 | 0.098030 | 0.005175 | 0.000135 | 0.000002 |
| 2 | 0.315884 | 0.088509 | 0.012041 | 0.001006 |
| 3 | 0.416254 | 0.420491 | 0.205303 | 0.063065 |
| 4 | 0.150220 | 0.432638 | 0.595139 | 0.522489 |
| 5 | 0.006924 | 0.052945 | 0.185505 | 0.401903 |
| 6 | 0.000008 | 0.000180 | 0.001878 | 0.011534 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of double-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.61 | 3 | 3 |
| Second Least | 3.44 | 3 | 4 |
| Third Least | 3.96 | 4 | 4 |
| Fourth Least | 4.36 | 4 | 4 |
Count of the Hottest Numbers in 300 Spins of Single-Zero Roulette
In 300 spins, the average number of wins on a single-zero wheel for any number is 300/37=8.11. The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.015727.
Count of the Hottest Four Numbers in 300 Spins on a Single-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000034 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000078 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000245 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000728 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.002069 | 0.000002 | 0.000000 | 0.000000 |
| 20 | 0.005570 | 0.000018 | 0.000000 | 0.000000 |
| 19 | 0.014191 | 0.000135 | 0.000000 | 0.000000 |
| 18 | 0.033833 | 0.000905 | 0.000008 | 0.000000 |
| 17 | 0.074235 | 0.005202 | 0.000125 | 0.000001 |
| 16 | 0.144490 | 0.025286 | 0.001624 | 0.000050 |
| 15 | 0.232429 | 0.097046 | 0.015727 | 0.001286 |
| 14 | 0.269735 | 0.259360 | 0.101259 | 0.021054 |
| 13 | 0.177216 | 0.382432 | 0.347102 | 0.175177 |
| 12 | 0.043266 | 0.208137 | 0.429715 | 0.508292 |
| 11 | 0.001879 | 0.021373 | 0.102979 | 0.283088 |
| 10 | 0.000003 | 0.000103 | 0.001461 | 0.011049 |
| 9 | 0.000000 | 0.000000 | 0.000000 | 0.000002 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.

Roulette Inside Odds On Jeopardy
Summary — Count of the Four Hottest Numbers — Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.74 | 15 | 14 |
| Second | 13.30 | 13 | 13 |
| Third | 12.50 | 12 | 12 |
| Fourth | 11.92 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Single-Zero Roulette
The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third coolest numbers will be observed five times is 0.287435.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.009926 | 0.000038 | 0.000000 | 0.000000 |
| 1 | 0.079654 | 0.003324 | 0.000068 | 0.000001 |
| 2 | 0.275226 | 0.062392 | 0.006791 | 0.000448 |
| 3 | 0.419384 | 0.350408 | 0.140173 | 0.034850 |
| 4 | 0.200196 | 0.484357 | 0.557907 | 0.406702 |
| 5 | 0.015563 | 0.098547 | 0.287435 | 0.521238 |
| 6 | 0.000050 | 0.000933 | 0.007626 | 0.036748 |
| 7 | 0.000000 | 0.000000 | 0.000001 | 0.000013 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of single-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Single-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.77 | 3 | 3 |
| Second Least | 3.62 | 4 | 4 |
| Third Least | 4.15 | 4 | 4 |
| Fourth Least | 4.56 | 5 | 5 |
The least I hope you have learned from this article is it is to be expected that certain numbers will come up more than others. To put it in other words, it is natural that some numbers will be 'hot' and some 'cool.' In fact, such differences from the mean are highly predictable. Unfortunately, for roulette players, we don't know which numbers will be 'hot,' just that some of them almost certainly will be. I would also like to emphasize, contrary to the Gambler's Fallacy, that on a fair roulette wheel that every number is equally likely every spin and it makes no difference what has happened in the past.
Finally, it should not be interpreted that we give an endorsement to the 888 Casino, which we linked to earlier. I am very bothered by this rule in their rule 6.2.B. Before getting to that, let me preface with a quote from rule 6.1, which I'm fine with.
Roulette Inside Odds On Ncaa Basketball
'If we reasonably determine that you are engaging in or have engaged in fraudulent or unlawful activity or conducted any prohibited transaction (including money laundering) under the laws of any jurisdiction that applies to you (examples of which are set out at section 6.2 below), any such act will be considered as a material breach of this User Agreement by you. In such case we may close your account and terminate the User Agreement in accordance with section 14 below and we are under no obligation to refund to you any deposits, winnings or funds in your account.' -- Rule 6.1
Let's go further now:
Roulette Inside Odds On Monday Night Football
The following are some examples of 'fraudulent or unlawful activity' -- Rule 6.2
Next, here is one of many examples listed as rule 6.2.B
'Unfair Betting Techniques: Utilising any recognised betting techniques to circumvent the standard house edge in our games, which includes but is not limited to martingale betting strategies, card counting as well as low risk betting in roulette such as betting on red/black in equal amounts.' -- Rule 6.2.B
Roulette Inside Odds Meaning
Let me make it perfectly clear that all betting systems, including the Martingale, not only can't circumvent the house edge, they can't even dent it. It is very mathematically ignorant on the part of the casino to fear any betting system. Why would any player trust this casino when the casino can seize all their money under the reason that the player was using a betting system? Any form of betting could be called a betting system, including flat betting. Casino 888 normally has a pretty good reputation, so I'm surprised they would lower themselves to this kind of rogue rule.
Roulette Inside Odds Games
Written by: Michael Shackleford